Задача коммивояжера — метод ветвей и границ

Одна из самых известных и важных задач транспортной логистики (и комбинаторной оптимизации) – задача коммивояжера или «задача о странствующем торговце» (англ. «Travelling Salesman Problem», TSP). Также встречается название «задача китайского почтальона» (англ. «Chinese Postman Problem», CPP). Суть задачи сводится к поиску оптимального (кратчайшего, быстрейшего или самого дешевого) пути, проходящего через промежуточный пункты по одному разу и возвращающегося в исходную точку. К примеру, нахождение наиболее выгодного маршрута, позволяющего коммивояжеру посетить со своим товаром определенные города по одному разу и вернуться обратно. Мерой выгодности маршрута может быть минимальное время поездки, минимальные расходы на дорогу или минимальная длина пути.

В наше время, когда стоимость доставки часто бывает сопоставима со стоимостью самого товара, а скорость доставки — один из главных приоритетов, задача нахождения оптимального маршрута приобретает огромное значение.

История появления и исследования задачи коммивояжера

Кто и когда впервые начал исследовать проблему задачи коммивояжера неизвестно, но уже в 1832 году была издана книга содержащая советы для коммивояжеров. В этой книге была описана задача нахождения кратчайшего пути для торговца или курьера, которому необходимо доставить товар в ряд городов, и предлагались примеры маршрутов. Однако, математический аппарат для решения задачи не приводился.

Одним из первых, кто сформулировал ранний вариант этой задачи, был выдающийся ирландский математик, физик и механик XIX в. — Уильям Роуэн Гамильтон. Ученый изучал симметрии икосаэдра (двадцатигранника) и в 1857 году предложил игру «Икосиан» (англ. «Icosian Game»), цель которой заключалась в прохождении всех вершин додекаэдра (двенадцатигранника) ровно по одному разу и только по его ребрам, с последующим возвратом в отправную точку. Иными словами нужно было найти так называемый гамильтонов цикл на графе с 20 узлами, в данном случае являющийся решением задачи и содержащий 20 ребер («двадцать» на древнегреческом «icosa», отсюда и название игры). Придуманную математиком головоломку продавали в Европе в виде доски с изображением додекаэдра и выемками на месте его вершин.

В 1930 году австрийско-американский математик Карл Менгер сформулировал задачу коммивояжера как «задачу найти кратчайший путь между конечным множеством мест, расстояние между которыми известно».

Современное название «задача коммивояжера» или «задача странствующего торговца» (англ. «Traveling Salesman Problem») было предложено американским математиком Хасслером Уитни.

Важный этап в развитии задачи коммивояжера наступил в 1950-1960 гг., когда ее исследованием занялись американские и европейские ученые. И здесь в первую очередь стоит отметить математиков Джорджа Данцига, Делберта Рея Фалкерсона и Селмера Джонсона. Именно они в 1954 году в институте RAND Corporation сформулировали проблему в качестве задачи дискретной оптимизации. Ученые применили метод отсечений (алгоритм Гомори) для решения частной задачи коммивояжера с 49 городами и обосновали оптимальность найденного маршрута.

Кроме того, в 1962 году китайский математик Мэй-Ку Куан изучал свою интерпретацию этой проблемы, получившей название «задача китайского почтальона» (англ. «Chinese Postman Problem»). В его варианте почтальону требовалось разнести письма по кратчайшему маршруту на вверенном ему участке города, проходя по каждой улице лишь единожды или с минимальным числом повторов.

В 1960-1970 гг. исследование задачи коммивояжера было продолжено, причем в 2-х направлениях: теоретическом и практическом (изучались возможности ее прикладного применения в экономике, биологии, химии, информатике).

В 1972 году американский ученый в сфере информатике Ричард Мэннинг Карп доказал NP-полноту задачи поиска гамильтоновых путей, из чего следовала NP-трудность задачи коммивояжера.

Плодотворными были 1970-1980 гг. когда Мартин Гретчел, Манфред Падберг, Джованни Ринальди и ряд других ученых, применяя новые разработки (метод деления плоскостью, метод ветвей и границ), смогли найти решение для задачи коммивояжера с 2392 городами.

Очередной рекорд по решению задачи коммивояжера установили в апреле 2006 года, когда было найдено решение для варианта с 85900 городами. Но это далеко не предел, используя определенные методы можно найти решение и для случая с миллионами городов!

Определение, условия и методы решения задачи коммивояжера

Задача коммивояжера — пожалуй, одна из самых известных оптимизационных задач. Ее цель заключается в нахождении самого выгодного маршрута (кратчайшего, самого быстрого, наиболее дешевого), проходящего через все заданные точки (пункты, города) по одному разу, с последующим возвратом в исходную точку.

Условия задачи должны содержать критерий выгодности маршрута (т. е. должен ли он быть максимально коротким, быстрым, дешевым или все вместе), а также исходные данные в виде матрицы затрат (расстояния, стоимости, времени и т. д.) при перемещении между рассматриваемыми пунктами.

Особенности задачи в том, что она довольно просто формулируется и найти хорошие решения для нее также относительно просто, но вместе с тем поиск действительно оптимального маршрута для большого набора данных — непростой и ресурсоемкий процесс.

Для решения задачи коммивояжера ее надо представить как математическую модель. При этом исходные условия можно записать в формате матрицы — таблицы, где строкам соответствуют города отправления, столбцам — города прибытия, а в ячейках указываются расстояния (время, стоимость) между ними; или в виде графа — схемы, состоящей из вершин (точек, кружков), которые символизируют города, и соединяющих их ребер (линий), длина которых соответствует расстоянию между городами.

Виды задачи коммивояжера по симметричности ребер графа:

• симметричная (англ. «Symmetric TSP») — все пары ребер, соединяющих одни и те же вершины, имеют одинаковую длину (т. е. граф, представляющий исходные данные задачи, является неориентированным). Иными словами, длина прямого пути от города A до города B и длина обратного пути от города B до города A, одинаковы. То же самое справедливо и в отношении остальных пар городов (A-C и C-A, B-C и C-D, и т. д.);
• асимметричная (англ. «Asymmetric TSP») — длина пар ребер соединяющих одни и те же города, может различаться (ориентированный граф). Для этого типа задачи коммивояжера прямой путь, например, из города A в город B может быть короче или длиннее обратного пути из города B в город A. Такое может быть не только в теории, но и в реальности — в случае дорог с односторонним движением.

Кроме того, в общем случае поиска кратчайшего пути охватывающего набор пунктов, которые требуется посетить по одному разу, говорят об обобщенной задаче коммивояжера (англ. «Generalized TSP»).

Типы задачи коммивояжера по замкнутости маршрута:

• замкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу с последующим возвратом в точку старта (маршрут получается замкнутым, закольцованным);
• незамкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу и без обязательного возврата в исходную точку (маршрут получается разомкнутым).

Можно предложить и другие классификации задачи коммивояжера (например, метрическая и неметрическая), но в данном случае не стоит перегружать ими статью.

В этой статье мы рассматриваем алгоритм решения именно для замкнутого варианта задачи (т. е. с возвратом в исходную точку).

Методы решения задачи коммивояжера довольно разнообразны и различаются применяемым инструментарием, точностью находимого решения и сложностью требуемых вычислений. Вот лишь некоторые из них:

• полный перебор (метод «грубой силы», англ. «Brute Force») — заключается в последовательном рассмотрении всех возможных маршрутов и выборе из них оптимального. Метод самый простой и точный, но неэффективный и при большом количестве городов его применение становится затруднительным ввиду значительных затрат времени и ресурсов на перебор огромного количества вариантов решения задачи. Для ускорения и повышения эффективности полного перебора используются различные приемы: метод ветвей и границ, параллельные вычисления, радужные таблицы;
• случайный перебор — в этом случае вычисляются не все возможные варианты маршрута, а лишь некоторые выбранные в случайном порядке (например, с помощью генератора случайных чисел). Из рассмотренных вариантов затем выбирается наилучший. Конечно, вероятнее всего полученное решение не будет оптимальным (впрочем, оно не будет и самым худшим), но зато данный метод требует меньших затрат времени и вычислительных ресурсов, а потому в некоторых случаях его применение оправдано;
• динамическое программирование — ключевая идея заключается в вычислении и запоминании пройденного пути от исходного города до всех остальных, последующем прибавлении к нему расстояний от текущих городов до оставшихся, и так далее. По сравнению с полным перебором этот метод позволяет существенно сократить объем вычислений;
• жадные алгоритмы (англ. «Greedy») — основаны на нахождении локально оптимальных решений на каждом этапе вычислений и допущении, что найденное таким образом итоговое решение будет глобально оптимальным. Т. е. на каждой итерации выбирается лучший участок пути, который включается в итоговый маршрут. Метод простой, но его большой недостаток в том, что может возникнуть ситуация, когда окажется, что начальная и конечная точки маршрута разнесены далеко друг от друга и их придется соединять длинным отрезком пути, что значительно снизит эффективность решения. К жадным алгоритмам относятся: метод ближайшего соседа (англ. «Nearest Neighbour»), модифицированный метод ближайшего соседа (англ. «Double Ended Nearest Neighbour»), метод самого дешевого включения и т. д.;
• метод минимального остовного дерева — поиск маршрута ведется на графе. Для нахождения оптимального пути применяются различные инструменты: алгоритм Прима, алгоритм Краскала, алгоритм Борувки;
• метод имитации отжига — один из численных методов Монте-Карло;
• метод эластичной сети — каждый из возможных маршрутов рассматривается как отображение окружности на плоскость;
• муравьиный алгоритм — эвристический метод, основанный на моделировании поведения муравьев, ищущих пути от своей колонии к источникам пищи. Первую версию такого алгоритма предложил доктор наук Марко Дориго в 1992 году. Этот метод позволяет относительно быстро найти хорошее, но не обязательно оптимальное решение;
• генетический алгоритм — еще один эвристический метод, заключающийся в случайном подборе и комбинировании исходных параметров с использованием механизмов имитирующих естественный отбор в процессе эволюции (наследование, мутации, кроссинговер). Несмотря на довольно широкие возможности применения (и не только в логистике), этот метод часто становится объектом критики;
• метод ветвей и границ — один из методов дискретной оптимизации, являющийся развитием метода полного перебора, но отличающийся от него отсевом в процессе вычисления подмножеств неэффективных решений. Впервые был предложен в 1960 году английским профессором Алисой Лэнд и австралийским математиком Элисон Дойг.

Ниже мы рассмотрим решение задачи коммивояжера с использованием метода ветвей и границ.

Общий план решения задачи коммивояжера

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующий алгоритм (последовательность действий):

1. Построение матрицы с исходными данными — в таблицу заносятся расстояния (C_ij) между городами (в ячейки типа A-A, B-B и т. д. ставится символ M — условно бесконечно большое число); при этом строкам соответствуют города отбытия, а столбцам города прибытия;
2. Нахождение минимумов по строкам — в каждой строке определяется минимальное число (d_i) и выписывается в отдельный столбец;
3. Редукция строк — из значений ячеек каждой строки вычитаем соответствующий минимум (C_ij = C_ij — d_i), не затрагивая при этом клетки с M;
4. Нахождение минимумов по столбцам — в каждом столбце определяется минимальное число (d_j) и выписывается в отдельную строку;
5. Редукция столбцов — из значений ячеек каждого столбца вычитаем соответствующий минимум (C_ij = C_ij — d_j), не затрагивая при этом клетки с M;
6. Нахождение корневой нижней границы (делаем это только один раз, в следующие разы пункт 6 пропускаем) — вычисляем нижнюю границу (минимально возможную на текущем этапе длину маршрута) в стартовой (корневой) точке решения, как сумму найденных ранее минимумов (H₀ = ∑d_i + ∑d_j) и начинаем построение графа (схемы) решения с внесения в него корневой вершины;
7. Вычисление оценок нулевых клеток — считаем оценки (p_ij) для каждой ячейки с нулями, как сумму минимумов по строке и столбцу, в которых располагается нулевая клетка, не учитывая при этом саму нулевую клетку;
8. Выбор нулевой клетки с максимальной оценкой — ищем среди нулевых клеток обладающую наибольшей оценкой (если таких ячеек несколько, выбираем любую), и получаем пару ветвей (вариантов) решения задачи: с включением в маршрут отрезка пути относящегося к выбранной ячейке и без включения;
9. Редукция матрицы — вычеркиваем относящиеся к выбранной клетке строку и столбец, а также заменяем значение ячейки соответствующей обратному пути на M;
10. Вычисление нижней границы первой ветви (включающей отрезок пути) — вновь находим минимумы по строкам, проводим редукцию строк, находим минимумы по столбцам, проводим редукцию столбцов, после чего вычисляем локальную нижнюю границу, как сумму предыдущей локальной нижней границы и минимумов (H_k = H_k-1 + ∑d_i + ∑d_j), и добавляем вершину в граф;
11. Вычисление нижней границы второй ветви (не включающей отрезок пути) — считаем локальную нижнюю границу, как сумму предыдущей локальной нижней границы и оценки выбранной ранее нулевой клетки (H_k^* = H_k-1 + p_ij), и добавляем вершину в граф;
12. Выбор ветви с минимальным значением нижней границы — среди еще не ветвившихся вершин выбираем обладающую минимальным значением локальной нижней границы (вне зависимости от того, какую ветвь рассматриваем в данный момент);
13. Если полный маршрут еще не найден, продолжаем решение, если найден — переходим к пункту 10 — если маршрут еще не найден, то ход дальнейшего решения зависит от выбранной ветви: (а) первая ветвь — переходим к пункту 7, (б) вторая ветвь — в клетку с максимальной оценкой ставим M и переходим к пункту 2, (в) другая ветвь — возвращаемся к соответствующим ей этапу решения и таблице данных;
14. Построение полного маршрута и определение его длины — соединяем все найденные ранее отрезки пути в полный маршрут и считаем его общую длину (данные берем из исходной таблицы) .

Это краткое описание методики решения задачи коммивояжера. Более подробно этапы вычисления оптимального маршрута описаны в примере ниже.

Подробная методика решения задачи коммивояжера

В целях лучшего понимания задачи будем оперировать не понятиями графа, его вершин и т. д., а понятиями простыми и максимально приближенными к реальности: вершины графа будут называться «города», ребра их соединяющие – «дороги».

Исходные данные для примера позаимствованы из одной статьи (указана в библиографии). Пример показался мне удобным для иллюстрации методики решения задачи коммивояжера, т. к. позволяет раскрыть некоторые нюансы и сложные методы.

В статье представлена авторская интерпретация метода ветвей и границ, не претендующая на абсолютную истину.

Итак, методика решения задачи коммивояжера методом ветвей и границ, с использованием алгоритма Литтла:

1. Построение матрицы с исходными данными

Сначала необходимо расстояния между городами (C_ij) представить в виде матрицы (таблицы). Конечно, кроме расстояний в таблице может быть указано время передвижения, стоимость перевозок или другие виды затрат.

Город	A	B	C	D	E
A	M	20	18	12	8
B	5	M	14	7	11
C	12	18	M	6	11
D	11	17	11	M	12
E	5	5	5	5	M

В рассматриваемом примере у нас 5 городов (обозначенных буквами латинского алфавита) и в таблице указано расстояние от каждого города к 4-м другим. Названия строк соответствуют городам отправления, названия столбцов — городам назначения. В ячейках, расположенных на пересечениях строк и столбцов, указано расстояние между соответствующими городами.

Обратите внимание, что в зависимости от направления движения расстояние между городами отличается (конечно в реальности расстояние при движении от пункта A к пункту B будет скорее всего одинаковым, но не обязательно: к примеру, пункты могут соединять дороги с односторонним движением различной длины; или, если мы говорим о стоимости, билеты на прямой и обратный рейс могут иметь разную цену).

Расстояние от города к этому же городу обозначено буквой M. Также используется знак бесконечности (∞) или сокращение «Inf» (от англ. «Infinity» — бесконечность). Это означает, что данный отрезок пути условно принят за бесконечно длинный. Тогда при решении задачи не будет математического смысла выбирать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т. п. в качестве отрезка итогового маршрута.

2. Нахождение минимумов по строкам

Находим минимальное значение в каждой строке (d_i) и выписываем его в отдельный столбец.

Город	A	B	C	D	E	di
A	M	20	18	12	8	8
B	5	M	14	7	11	5
C	12	18	M	6	11	6
D	11	17	11	M	12	11
E	5	5	5	5	M	5

В первой строке у нас имеются такие значения как: M, 20, 18, 12 и 8. Как было сказано выше, символ M означает бесконечно большое число. Поэтому минимум по первой строке — 8. Точно также находим минимумы по остальным строкам.

Найденные значение d_i называются константами приведения для строк.

3. Редукция строк

Производим редукцию строк – из каждого элемента в каждой строке вычитаем соответствующее ей значение минимума (C_ij = C_ij — d_i).

Город	A	B	C	D	E	di
A	M	12	10	4	0	8
B	0	M	9	2	6	5
C	6	12	M	0	5	6
D	0	6	0	M	1	11
E	0	0	0	0	M	5

Например, в ячейке A-B (ячейку A-A и другие клетки с M не трогаем) у нас было число 20. После редукции (20 — 8) получаем новое значение 12. Затем для остальных ячеек первой строки: 18 — 8 = 10, 12 — 8 = 4, 8 — 8 = 0, и в том же духе для ячеек других строк.

В итоге получаем таблицу с новыми данными, в каждой строке которой будет хотя бы одна нулевая клетка.

4. Нахождение минимумов по столбцам

Далее находим минимальные значения в каждом столбце (d_j). Эти минимумы (включая нули) выписываем в отдельную строку.

Город	A	B	C	D	E
A	M	12	10	4	0
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	0	0	0	M
dj	0	0	0	0	0

К примеру, в первом столбце имеются следующие значения: M, 0, 6, 0 и 0. Наименьшее среди них — 0, его и выписываем в отдельную строку. Аналогичные действия осуществляем для остальных столбцов.

Найденные значение d_j называются константами приведения для столбцов. Так совпало, что здесь все они нулевые, но конечно их значения могут быть и больше нуля (но никак не отрицательными).

5. Редукция столбцов

Производим редукцию столбцов — вычитаем из каждого элемента каждого столбца соответствующее ему значение минимума (C_ij = C_ij — d_j).

Город	A	B	C	D	E
A	M	12	10	4	0
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	0	0	0	M
dj	0	0	0	0	0

Например, ячейка B-A после редукции (0 — 0) будет равна 0. Далее для остальных ячеек первого столбца: 6 — 0 = 6, 0 — 0 = 0, 0 — 0 = 0 и т. д. Напоминаю, что ячейки с M при редукции не меняются.

В итоге в каждом столбце будет хотя бы одна нулевая клетка.

6. Нахождение корневой нижней границы

На этом этапе следует провести небольшое, но крайне важное вычисление, а именно определить корневую локальную нижнюю границу (H_k) длины (стоимости, длительности) маршрута. Для этого нужно суммировать константы приведения d_i и d_j.

Обратите внимание, что мы не вычисляем заново константы приведения для строк, а используем найденные ранее значения.

Город	A	B	C	D	E	di
A	M	12	10	4	0	8
B	0	M	9	2	6	5
C	6	12	M	0	5	6
D	0	6	0	M	1	11
E	0	0	0	0	M	5
dj	0	0	0	0	0

Формула для вычисления локальной нижней границы в корневой (стартовой) точке решения следующая (далее мы будем использовать несколько отличающиеся формулы): H₀ = ∑d_i + ∑d_j.

Считаем: H₀ = (8 + 5 + 6 + 11 + 5) + (0 + 0 + 0 + 0 + 0) = 35 + 0 = 35.

Найденное значение H = 35 является текущей или локальной нижней границей. Вообще, при последующих вычислениях H к предыдущему значению локальной нижней границы прибавляется новое значение локальной нижней границы, но этот момент разберем ниже. В же первый раз, нижняя граница вычисляется просто как сумма констант приведения.

Корневую локальную нижнюю границу считаем только единожды! В последующие разы этот пункт пропускаем.

Ход решения задачи коммивояжера удобно представить в виде графа, где вершинами будут ключевые решения по включению / невключению в итоговый маршрут тех или иных отрезков пути, а ребра показывающие ход решения, образуют ветви альтернативных вариантов маршрута. Пока у нас есть только одна вершина — «корень» дерева решения, куда мы вписываем значение локальной нижней границы H = 35.

Отмечу, что по сути значение H, это ни что иное как текущая минимальная длина маршрута. Т. е. короче вычисляемый маршрут быть не может, длиннее — возможно.

7. Вычисление оценок нулевых клеток

Для каждой нулевой клетки преобразованной матрицы находим «оценку» (p_ij). Ею будет сумма минимума по строке и минимума по столбцу, на пересечении которых находится данная клетка с нулем. При этом сама нулевая клетка для которой вычисляется оценка и найденные ранее d_i и d_j НЕ учитываются (но другие нулевые клетки, если они есть в рассматриваемых строке и столбце, учитывать нужно; также учитываются ячейки с M, которые означают бесконечно большое число). Полученную оценку записываем рядом с нулем, в скобках.

Например, первая строка таблицы содержит одну нулевую клетку A-E. Вычислим для нее оценку: 4 (минимальное значение среди ячеек строки) + 1 (минимальное значение среди ячеек столбца) = 5.

Город	A	B	C	D	E
A	M	12	10	4	0 (5)
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	0	0	0	M

Аналогично находим оценки для всех остальных нулевых клеток:

Город	A	B	C	D	E
A	M	12	10	4	0 (5)
B	0 (2)	M	9	2	6
C	6	12	M	0 (5)	5
D	0 (0)	6	0 (0)	M	1
E	0 (0)	0 (6)	0 (0)	0 (0)	M

Вычисленные нами оценки также называются штрафами за НЕиспользование тех отрезков маршрута, которым соответствуют клетки с нулями (напоминаю, что каждая клетка «указывает» на два города: по своей строке — на город из которого выезжаем, и по своему столбцу — на город в который приезжаем). Штраф указывают на затраты расстояния, времени, стоимости (или иного параметра, в целях оптимизации которого мы решаем задачу коммивояжера), которые появятся если НЕ выбрать данную клетку.

8. Выбор нулевой клетки с максимальной оценкой

Следующий важный шаг — выбор среди нулевых клеток матрицы той, что имеет наибольшую оценку. Это делается для того, чтобы избежать максимального удлинения маршрута, которое появится если НЕ выбрать такую ячейку.

Город	A	B	C	D	E
A	M	12	10	4	0 (5)
B	0 (2)	M	9	2	6
C	6	12	M	0 (5)	5
D	0 (0)	6	0 (0)	M	1
E	0 (0)	0 (6)	0 (0)	0 (0)	M

В нашем случае максимальную оценку имеет клетку E-B. Этой ячейке соответствует отрезок пути от города E к городу B.

Стоит отметить, что когда не одна, а несколько нулевых ячеек имеют одинаковую максимальную оценку, можно выбрать любую из них.

9. Редукция матрицы

На этом этапе решение задачи начинает ветвиться. Возникает развилка с парой альтернативных вариантов:

• ветвь решения, где мы включаем в маршрут выбранный отрезок пути (E-B);
• и ветвь, где мы его в маршрут НЕ включаем.

Для начала рассмотрим первую ветвь решения, предусматривающую включение отрезка в маршрут. Для проверки этого варианта необходимо провести редукцию матрицы. Делается это следующим образом: выбрав клетку с максимальной оценкой, вписываем в нее букву M, и затем полностью вычеркиваем соответствующие ей строку и столбец.

В нашем примере мы включаем в итоговый маршрут движение из города E в город B. Следовательно, из города E в другие города выезжать уже не будем, а в город B по условиям задачи дважды заезжать нельзя. Поэтому данные строка и столбец нам более не понадобятся.

Город	A	B	C	D	E
A	M	12	10	4	0
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	M	0	0	M

Важный момент! В клетку соответствующую обратному пути (B-E) ставим еще одну М (т. к. мы уже не будем возвращаться обратно из города B в город E).

Город	A	C	D	E
A	M	10	4	0
B	0	9	2	M
C	6	M	0	5
D	0	0	M	1

В результате редукции (исключения строки и столбца нулевой клетки с максимальной оценкой) получаем новую уменьшенную таблицу.

10. Вычисление нижней границы первой ветви

Теперь необходимо вычислить локальную нижнюю границу для первой ветви решения задачи, предполагающей включение в итоговый маршрут выбранного отрезка пути (у нас это E-B).

Чтобы это сделать, для новой таблицы вновь находим минимумы по строкам и проводим редукцию строк.

Город	A	C	D	E	di
A	M	10	4	0	0
B	0	9	2	M	0
C	6	M	0	5	0
D	0	0	M	1	0

Далее находим минимумы по столбцам и проводим редукцию столбцов.

Город	A	C	D	E
A	M	10	4	0
B	0	9	2	M
C	6	M	0	5
D	0	0	M	1
dj	0	0	0	0

Затем вычисляем значение локальной нижней границы по формуле: H_k = H_k-1 + ∑d_i + ∑d_j.

Как видите, в этом случае локальная нижняя граница рассчитывается немного не так, как в пункте 6. Здесь это сумма предыдущей локальной нижней границы ветвящейся вершины (т. е. того участка графа, из которого исходят рассматриваемые ветви) и констант приведения: H₁ = 35 + (0 + 0 + 0 + 0) + (0 + 0 + 0 + 0) = 35. Полученное значение — локальная нижняя граница для данной ветви решения. Оно означает, что включение отрезка пути E-B на данном этапе не приводит к удлинению итогового маршрута (поскольку корневая нижняя граница также равна 35).

11. Вычисление нижней границы для второй ветви

Далее необходимо проверить вторую ветвь — вычислим для нее значение локальной нижней границы. В этом случае мы НЕ исключаем из таблицы отрезок E-B и локальная нижняя граница будет равна сумме предыдущей локальной нижней границы и максимальной оценки (т. е. оценки той нулевой клетки, которую мы выбрали на предыдущем шаге): H_k^* = H_k-1 + p_ij.

Т. о. локальная нижняя граница для второй ветви (пометим ее звездочкой) составит H₁^* = 35 + 6 = 41. Как видите, данная ветвь решения увеличивает минимально возможную длину итогового маршрута до значения 41.

12. Выбор ветви с минимальным значением нижней границы

Прежде всего, для наглядности, добавим обе рассмотренных ветви решения задачи в граф. Здесь рассматриваемая пара ветвей исходит из корневой вершины. Запишем для каждой ветви относящийся к ней отрезок пути (звездочками помечена ветвь в которой отрезок пути НЕ включен в итоговый маршрут) и значение локальной нижней границы.

Теперь из всех (!) НЕ ветвившихся вершин графа выбираем ту, что имеет наименьшее значение локальной нижней границы.

Еще раз обращаю ваше внимание, что мы учитываем только те вершины (прямоугольники на рисунке), которые еще НЕ ветвились. К примеру, на данном этапе корень дерева решения уже ветвился и мы его не учитываем, поэтому выбор ведется среди двух ветвей заканчивающихся вершинами E^*-B^* и E-B.

Важный нюанс — при выборе следует рассматривать не только проверяемую в текущий момент пару ветвей, но и все другие ветви, даже отринутые на предыдущих этапах (пока таких нет, но далее по ходу решения задачи подобный случай будет разобран подробнее).

Поскольку в нашем примере пока всего две ветви и та, что включает в маршрут отрезок E → B, имеет значение локальной нижней границы меньше, чем в случае альтернативного варианта (35 < 41), выбираем ее.

13. Если полный маршрут еще не найден, продолжаем решение задачи, если найден — переходим к пункту 14

Если мы еще не нашли все отрезки пути, то продолжаем решение задачи и здесь возможны 3 варианта:

1. выбор ветви включающей рассматриваемый отрезок — в этом случае решение задачи продолжается с пункта 7. Вновь находить минимумы по строкам и столбцам, а также проводить редукцию строк и столбцов не нужно, т. к. все это уже было сделано при вычислении локальной нижней границы в пункте 10. Поэтому сразу переходим к этапу вычисления оценок нулевых клеток;
2. выбор ветви НЕ включающей рассматриваемый отрезок — такой вариант предусматривает исключение из итогового маршрута искомого отрезка, для чего в соответствующую ему клетку таблицы необходимо поставить M. Затем возвращаемся к пункту 2 и продолжаем решение задачи;
3. выбор другой ветви — здесь мы возвращаемся к соответствующим этой ветви этапу решения и таблице с данными.

В нашем случае мы выбрали вариант с включением в итоговый маршрут ветви содержащей отрезок пути E-B, а значит вновь находить минимумы по строкам и столбцам, а также проводить их редукцию не нужно — это мы уже делали ранее. Поэтому сразу вычисляем оценки для нулевых клеток и определяем ячейку с максимальной (D-C).

Город	A	C	D	E
A	M	10	4	0 (5)
B	0 (2)	9	2	M
C	6	M	0 (7)	5
D	0 (0)	0 (9)	M	1

Рассматриваем два варианта: с включением ветви D → C в маршрут и без этой ветви. В последнем случае, как мы подсчитали выше, локальная минимальная нижняя граница будет равна H^* = 35 (предыдущая локальная нижняя граница) + 9 (максимальная оценка нулевой клетки) = 44.

Рассмотрим теперь первый вариант, предусматривающий включение ветви D-C в маршрут. Для этого проводим редукцию матрицы и ставим M на обратный путь (C-D).

Город	A	D	E
A	M	4	0
B	0	2	M
C	6	M	5

Вычисляем минимумы по строкам.

Город	A	D	E	di
A	M	4	0	0
B	0	2	M	0
C	6	M	5	5

Проводим редукцию строк.

Город	A	D	E	di
A	M	4	0	0
B	0	2	M	0
C	1	M	0	5

Находим минимумы по столбцам.

Город	A	D	E
A	M	4	0
B	0	2	M
C	1	M	0
dj	0	2	0

Проводим редукцию столбцов.

Город	A	D	E
A	M	2	0
B	0	0	M
C	1	M	0
dj	0	2	0

Определяем локальную нижнюю границу: H = 35 + (0 + 0 + 5) + (0 + 2 + 0) = 42.

Не забываем отметить оба варианта в нашем графе.

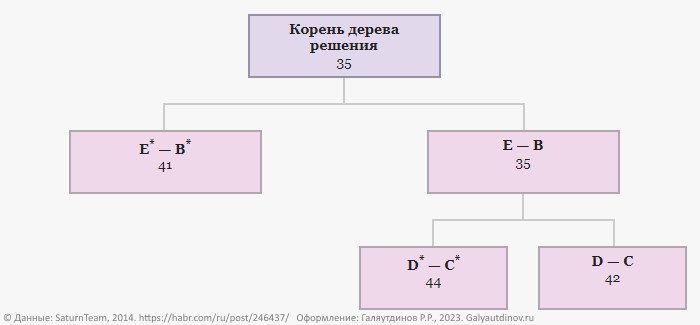
Теперь выбираем из всех еще не ветвившихся вершин ту, что имеет наименьшее значение локальной нижней границы. Здесь этому условию отвечает вершина E^* — B^*, которая имеет локальную нижнюю минимальную границу равную 41. Поэтому нам необходимо вернуться и продолжить развитие этой ветви решения задачи.

Если мы отбрасываем одну из ветвей и возвращаемся обратно, нам необходимо эту ветвь полностью исключить для дальнейшего рассмотрения, поэтому в соответствующую ей ячейку нужно поставить M, а также заново определить константы приведения и провести новую редукцию строк и столбцов!

Итак, возвращаемся по графу к ветви НЕ предусматривающей включение отрезка E-B в итоговый маршрут. Поскольку, данный отрезок пути был нами отвергнут, необходимо поставить в ячейку E-B символ M.

Город	A	B	C	D	E
A	M	12	10	4	0
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	M	0	0	M

Определяем минимумы по строкам.

Город	A	B	C	D	E	di
A	M	12	10	4	0	0
B	0	M	9	2	6	0
C	6	12	M	0	5	0
D	0	6	0	M	1	0
E	0	M	0	0	M	0

Проводим редукцию строк. Т. к. минимумы или иначе константы приведения для строк (d_i) нулевые, данные не изменятся.

Город	A	B	C	D	E	di
A	M	12	10	4	0	0
B	0	M	9	2	6	0
C	6	12	M	0	5	0
D	0	6	0	M	1	0
E	0	M	0	0	M	0

Определяем минимумы по столбцам.

Город	A	B	C	D	E
A	M	12	10	4	0
B	0	M	9	2	6
C	6	12	M	0	5
D	0	6	0	M	1
E	0	M	0	0	M
dj	0	6	0	0	0

Проводим редукцию столбцов.

Город	A	B	C	D	E
A	M	6	10	4	0
B	0	M	9	2	6
C	6	6	M	0	5
D	0	0	0	M	1
E	0	M	0	0	M
dj	0	6	0	0	0

Вычисляем оценки нулевых клеток преобразованной матрицы и выбираем среди них максимальную.

Город	A	B	C	D	E
A	M	6	10	4	0 (5)
B	0 (2)	M	9	2	6
C	6	6	M	0 (5)	5
D	0 (0)	0 (6)	0 (0)	M	1
E	0 (0)	M	0 (0)	0 (0)	M

Здесь клетка с максимальной оценкой D-B. Проводим редукцию матрицы, вычеркивая соответствующие этой ячейке строку и столбец. Не забываем поставить на обратный путь (B-D) букву M.

Город	A	C	D	E
A	M	10	4	0
B	0	9	M	6
C	6	M	0	5
E	0	0	0	M

Найдем константы приведения, а также проведем редукцию строк и столбцов для новой таблицы.

Город	A	C	D	E	di
A	M	10	4	0	0
B	0	9	M	6	0
C	6	M	0	5	0
E	0	0	0	M	0
dj	0	0	0	0

Здесь минимумы по строкам и столбцам равны 0, а следовательно данные не меняются. Далее определим локальную нижнюю границу: H = 41 + (0 + 0 + 0 + 0) + (0 + 0 + 0 + 0) = 41.

Что касается варианта не предусматривающего включение отрезка D-B в итоговый маршрут, то для него H^* = 41 + 6 = 47. Занесем все эти данные в граф.

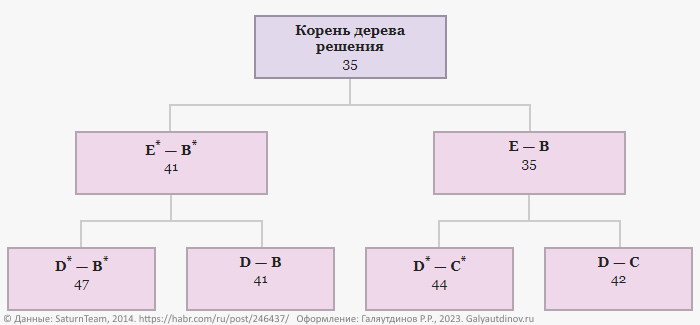
Поскольку 41 меньше, чем локальные нижние границы других ветвей, выбираем данную ветвь, предусматривающую включение в итоговый маршрут отрезка D-B.

Продолжаем решение задачи. Теперь следует вычислить оценки нулевых клеток и определить среди них максимальную.

Город	A	C	D	E
A	M	10	4	0 (9)
B	0 (6)	9	M	6
C	6	M	0 (5)	5
E	0 (0)	0 (9)	0 (0)	M

Вновь у нас две клетки с одинаковой максимальной оценкой равной 9: A-E и E-C. Выбираем любую, например A-E.

Проверяем новые ветви: с включением в итоговый маршрут отрезка A-E и без этого отрезка пути.

Для варианта с включением отрезка в маршрут проводим редукцию матрицы, а также исключаем обратный путь (E-A).

Город	A	C	D
B	0	9	M
C	6	M	0
E	M	0	0

Находим минимумы по строкам — везде 0, проводим редукцию строк (данные, понятное дело, в этом случае не изменятся). Находим минимумы по столбцам — также 0, проводим редукцию столбцов (данные остаются прежними).

Считаем H = 41 + (0 + 0 + 0) + (0 + 0 + 0) = 41.

Для ветви не включающей отрезок пути A-E значение H^* = 41 + 9 = 50.

Занесем все эти данные в граф.

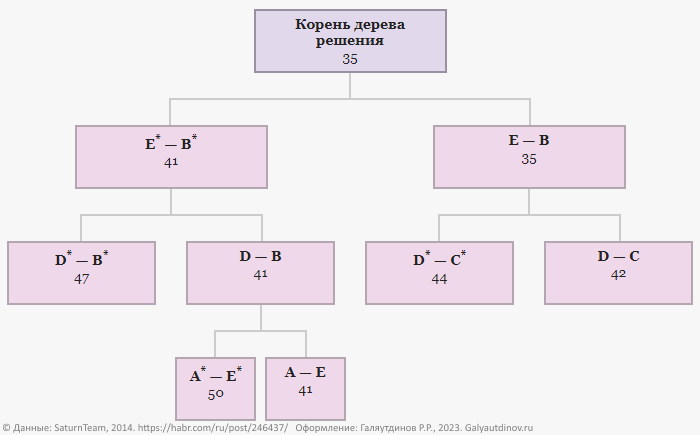
Т. к. нет других ветвей решения со значением локальной нижней границы меньше 41, выбираем ветвь с включением отрезка пути A-E в итоговый маршрут и продолжаем ее решение.

Переходим к этапу вычисления оценок нулевых клеток и определения максимальной среди них.

Город	A	C	D
B	0 (15)	9	M
C	6	M	0 (6)
E	M	0 (9)	0 (0)

Ячейка B-A имеет максимальную оценку 9, поэтому выбираем ее. Проводим редукцию матрицы. Исключать обратный путь (A-B) нужды нет, поскольку такая ячейка в таблице отсутствует.

Город	C	D
C	M	0
E	0	0

Найдем для новой таблицы минимумы по строкам (везде 0) и столбцам (также 0). Данные, в результате редукции строк и столбцов, не изменятся.

Вычислим локальную нижнюю границу для ветви включающей отрезок B-A: H = 41 + (0 + 0) + (0 + 0) = 41.

В то же время локальная нижняя граница для ветви не включающей отрезок B-A равна: H^* = 41 + 15 = 56.

Добавим оба варианта в граф.

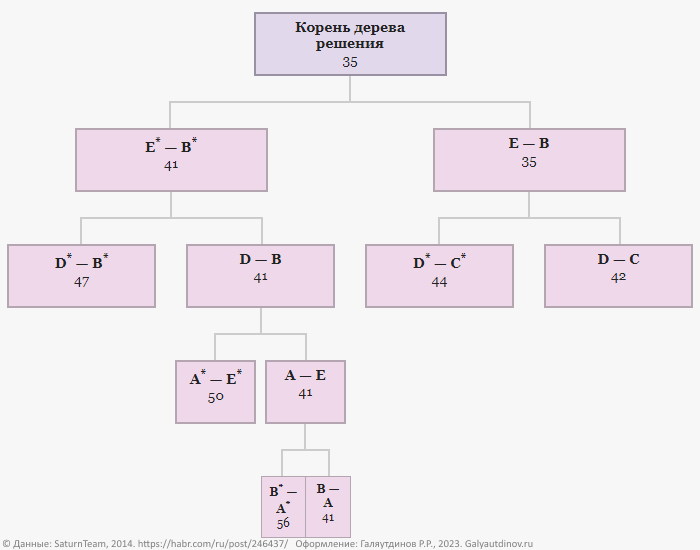
Ветвь, включающая отрезок B-A в итоговый маршрут, имеет локальную нижнюю границу 41. Это меньше, чем соответствующие значения других ветвей, следовательно продолжаем решение ветви с вершиной B-A.

Вычислим оценки для нулевых клеток и найдем среди них максимальную.

Город	C	D
C	M	0 (∞)
E	0 (∞)	0 (0)

Здесь две клетки (C-D и E-C) имеют максимальное значение оценки, которое бесконечно велико (напомню, что M означает бесконечно большое число, и, к примеру, в строке C оно является минимумом, т. к. саму нулевую клетку при подсчете оценки не учитываем, а других клеток в этой строке нет). Выбираем любую из этих двух ячеек, допустим, C-D.

Проводим редукцию матрицы. Обратного пути в таблице нет, поэтому исключать его нужды нет.

Город	C
E	0

Минимумы по строкам и столбцам — нулевые, редукция строк и столбцов данные не изменит.

Определим локальную нижнюю границу для ветви включающей отрезок C-D: H = 41 + (0) + (0) = 41.

Тогда локальная нижняя граница для варианта не включающего отрезок C-D будет: H^* = 41 + ∞ = ∞. Занесем новые данные в граф.

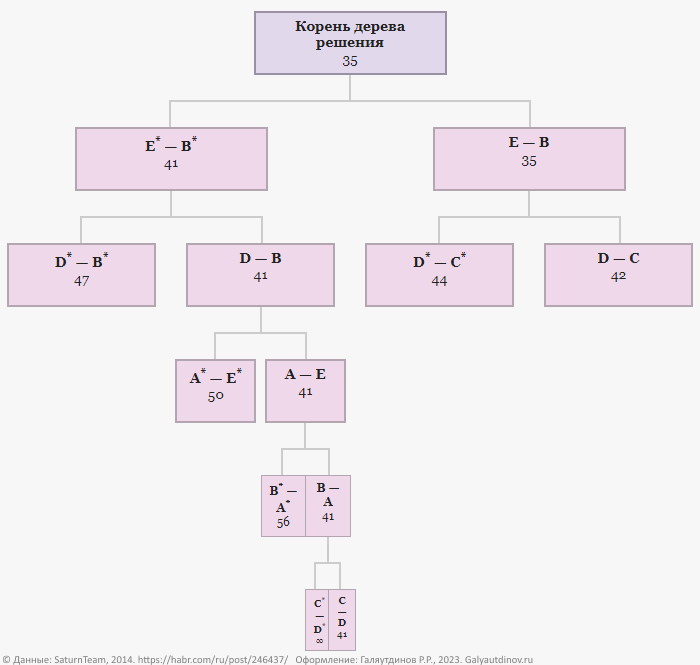
Новая ветвь включающая отрезок C-D имеет локальную нижнюю границу 41, что меньше значений вершин остальных ветвей. Поэтому выбираем ветвь с отрезком пути C-D.

В матрице осталась единственная ячейка E-C. Альтернатив нет, поэтому добавляем в маршрут и этот участок пути.

Город	C
E	0

На этом основная часть решения задачи может считаться завершенной и мы переходим к последнему пункту 14.

14. Построение полного маршрута и определение его длины

Найдя все отрезки пути, остается только соединить их между собой и рассчитать общую длину пути (стоимость поездки по этому маршруту, затраченное время и т. д.). Расстояния между городами берем из самой первой таблицы с исходными данными.

В нашем примере в ходе решения задачи коммивояжера мы нашли следующие участки пути: D-B (17), A-E (8), B-A (5), C-D (6) и E-C (5). В скобках указано расстояние между городами. Упорядочим и соединим эти отрезки, тогда маршрут получится следующий: A → E → C → D → B → A.

Общая длина пути: L = ∑C_ij = 8 + 5 + 6 + 17 + 5 = 41. Обратите внимание, что длину маршрута мы уже знали, это самое последнее значение локальной нижней границы правильной ветви решения.

Практическая и теоретическая значимость задачи коммивояжера

Применение задачи коммивояжера довольно обширно. Вот лишь некоторые возможные варианты применения задачи коммивояжера на практике в экономике:

• определение оптимального маршрута грузоперевозок;
• расчет наилучших маршрутов для курьеров и почтальонов.

Кроме логистики, задачи коммивояжера находит применение и в других областях экономики и человеческой деятельности: финансы (оптимизация денежных потоков, например, поиск путей перевода денежных средств с минимальными транзакционными издержками), туризм (расчет маршрутов экскурсий и туров), шоу-бизнес (организация турне музыкальных групп), биология (сборка генома), телекоммуникации и связь (управление спутникам, проектирование телекоммуникационных сетей), информатика (кластеризация массивов данных), энергетика и коммунальное хозяйство (соединение населенных пунктов линиями электропередач и газоснабжения), электроника (проектирование топологий микросхем).

Кроме практического смысла задача имеет большую теоретическую значимость. В частности, она выступает моделью для проверки новых методов оптимизации, поскольку нахождение по-настоящему оптимального маршрута для большого количества рассматриваемых пунктов является сложной проблемой требующей эффективных математических инструментов. Немало современных и востребованных методов дискретной оптимизации (рассмотренный нами метод ветвей и границ, метод отсечений, эвристические алгоритмы) были разработаны именно на примере задачи коммивояжера.

Решение задачи коммивояжера онлайн

Иногда бывает необходимо быстро просчитать какой-либо вариант для этой задачи или проверить правильность решения. На этот случай я создал сервис для решения задачи коммивояжера онлайн. Воспользоваться им можно перейдя по приведенной здесь ссылке.

Галяутдинов Р.Р.

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.