Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.
Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.
Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.
Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Теоретический материал по транспортной задаче
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Математическая модель транспортной задачи имеет следующий вид:
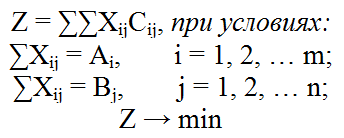
где: Z — затраты на перевозку грузов;
X — объем груза;
C — стоимость (тариф) перевозки единицы груза;
A — запас поставщика;
B — запрос потребителя;
m — число поставщиков;
n — число потребителей.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Ниже приведен алгоритм решения транспортной задачи в самом общем виде:
- Построение транспортной таблицы.
- Проверка задачи на закрытость.
- Составление опорного плана.
- Проверка опорного плана на вырожденность.
- Вычисление потенциалов для плана перевозки.
- Проверка опорного плана на оптимальность.
- Перераспределение поставок.
- Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
- Вычисление общих затрат на перевозку груза.
- Построение графа перевозок.
Подробная инструкция по решению транспортной задачи
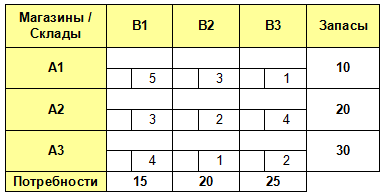
1. Построение транспортной таблицы
Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).
2. Проверка задачи на закрытость
Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.
Тогда:
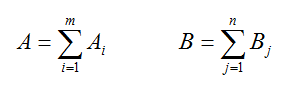
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.
Проверим задачу на закрытость:
A = 10 + 20 + 30 = 60.
B = 15 + 20 + 25 = 60.
A = B, следовательно данная транспортная задача — закрытая.
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
Подробное описание метода и пример можно посмотреть здесь.
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным тарифом. Затем выбирается следующая клетка с наименьшим значением тарифа и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть здесь
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.
Подробное описание метода и пример можно посмотреть здесь
Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).
Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
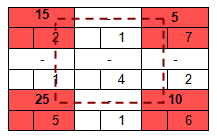
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.
В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.
Следовательно, первоначальный план перевозок — невырожденный (5 = 5).
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj соответствующие величины Ui и Vj так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: Ui + Vj = Cij.
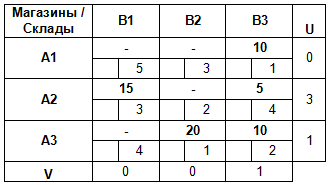
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
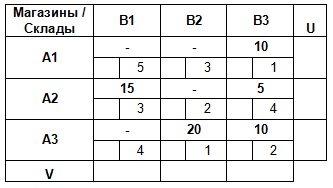
Предположим, что U1 = 0.
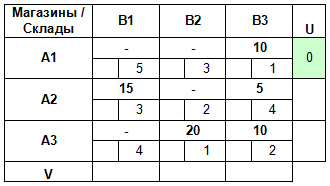
Тогда мы сможем найти V3 = C13 — U1 = 1 — 0 = 1.
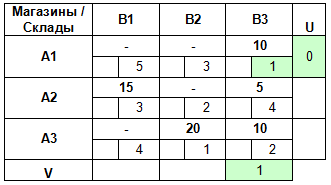
Зная V3, мы теперь можем найти U3:
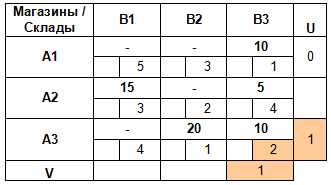
По аналогии вычисляем все оставшиеся потенциалы:
6. Проверка плана на оптимальность методом потенциалов
Для каждой свободной клетки плана вычислим разности ΔCij = Cij — (Ui + Vj ), и запишем полученные значения в левых нижних углах соответствующих ячеек.
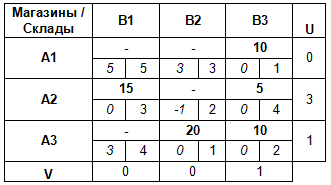
План является оптимальным, если все разности ΔCij ≥ 0.
В данном случае план — неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.
7. Перераспределение поставок
Найдем ячейку с наибольшей по абсолютной величине (т. е. без учета знака, по модулю) отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.
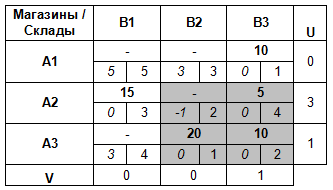
Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «-», и так далее, поочередно.
Затем находим минимальное значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).
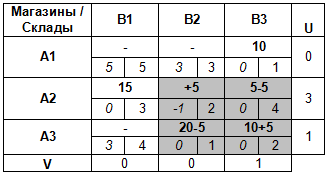
Получим новый опорный план перевозок:
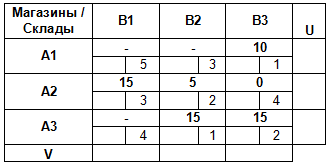
Так как базисных клеток стало больше, чем m + n — 1, то базисную клетку с нулевым значением делаем свободной:
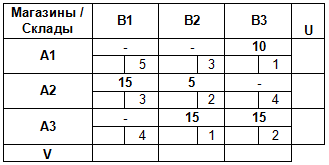
Снова вычисляем значения потенциалов и разности ΔCij:
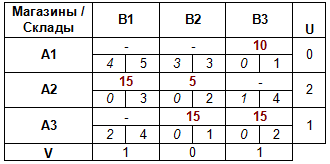
На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.
8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
В нашем примере оптимальное решение найдено, поэтому переходим к пункту 9.
9. Вычисление общих затрат на перевозку груза
Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:
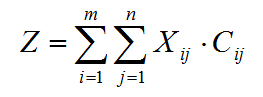
То есть нужно перемножить значения объемов грузоперевозок на соответствующие им тарифы.
Zmin = 10 ⋅ 1 + 15 ⋅ 3 + 5 ⋅ 2 + 15 ⋅ 1 + 15 ⋅ 2 = 110 ден. ед.
В результате общие затраты на доставку всей продукции для оптимального решения составляют 110 ден. ед.
10. Построение графа перевозок
Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
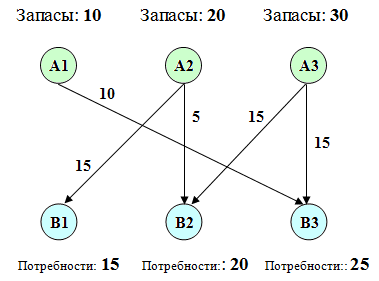
Все, транспортная задача решена. Поздравляю!
Практическое применение транспортной задачи
Транспортная задача применяется во многих случаях. В частности:
- оптимизация поставок сырья и материалов на производственные предприятия;
- оптимизация доставок товаров со складов в розничные магазины;
- оптимизация пассажирских перевозок.
Это далеко не полный перечень возможностей прикладного использования транспортной задачи.
- Галяутдинов Р. Р. Конспект лекций по логистике
- Решение транспортной задачи в 1С: Предприятие 8.2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
- Транспортная задача // Википедия. URL: http://ru.wikipedia.org/wiki/Транспортная_задача (дата обращения: 29.10.2013)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.