 Среди четырех, чаще всего применяющихся на практике, методов формирования опорного плана в транспортной задаче самый необычный — метод аппроксимации Фогеля. Последовательность действий при его использовании совершенно иная, чем при заполнении транспортной таблицы методом «Северо-Западного угла» или методом «Минимального элемента».
Среди четырех, чаще всего применяющихся на практике, методов формирования опорного плана в транспортной задаче самый необычный — метод аппроксимации Фогеля. Последовательность действий при его использовании совершенно иная, чем при заполнении транспортной таблицы методом «Северо-Западного угла» или методом «Минимального элемента».
На первый взгляд аппроксимация Фогеля сложнее, но это ложное впечатление. Метод простой и позволяет получить опорный план более приближенный к оптимальному решению, чем в случае применения других методов (за исключением разве что метода «Двойного предпочтения»).
Сущность аппроксимации Фогеля в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем строка или столбец с наибольшей разностью заполняются в направлении от клетки с минимальным тарифом к клетке с максимальным. Подробнее далее.
Формирование опорного плана методом аппроксимации Фогеля
Первым делом находим для каждой строки транспортной таблицы абсолютные разности (по модулю, т. е. без знака) между двумя минимальными тарифами в этой строке. То же самое делаем и для каждого столбца: ищем в нем два минимальных тарифа и находим их разность по модулю.
Если в строке/столбце две клетки с одинаковыми и минимальными значениями тарифов, то берем именно их. Тогда разность будет равна 0.
Найденные разности выписываем в добавочный столбец (Δi) и добавочную строку (Δj).
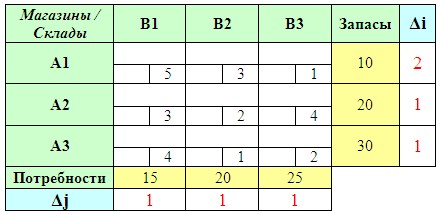
Среди вычисленных разностей (и по строкам, и по столбцам!) выбираем наибольшую.
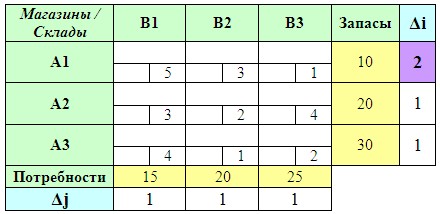
Затем в строке или столбце, которому соответствует максимальная разность, ищем клетку с минимальным тарифом. Заполняем ее максимально возможным объемом грузоперевозки.
Если клеток с минимальным тарифом несколько, то заполняем ту из них, которой соответствует наибольшая разность (Δj — если выбираем по строке, или Δi — если выбираем по столбцу).
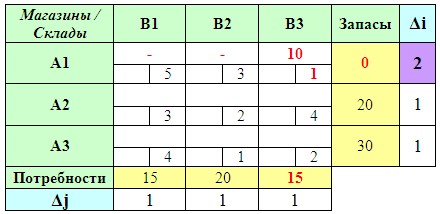
Затем повторяем все вышеописанные действия снова, только уже не учитывая заполненные клетки и выбранные ранее разности (Δi и Δj). И так до тех пор, пока не будет полностью найден опорный план.
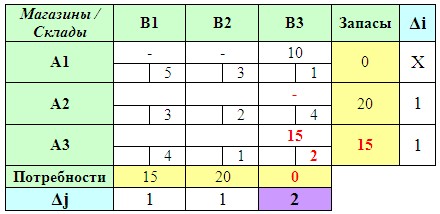
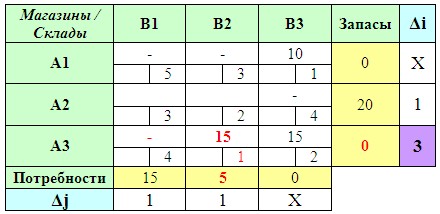
Оставшиеся ячейки транспортной матрицы уже и так очевидно каким образом следует заполнить:
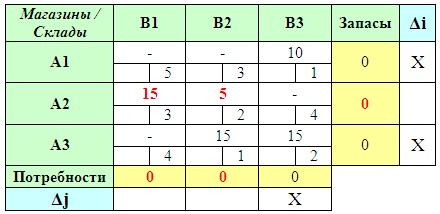
В результате мы получаем опорный план:
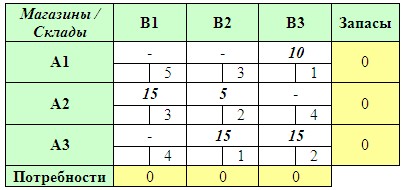
Зачастую опорный план, полученный аппроксимацией Фогеля, оказывается либо сразу оптимальным (как в этом примере), либо очень близким к нему. Но именно часто, а не всегда!
- Аппроксимация Фогеля // Викиучебник. URL: http://ru.wikibooks.org/wiki/Аппроксимация_Фогеля (дата обращения: 5.03.2014)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.